الفيبوناتشي – Fibonacci

الفيبوناتشي – Fibonacci | مستويات فيبوناتشي | نسب فيبوناتشي

ليوناردو بيسانو، أو ليوناردو فيبوناتشي كما هو معروف على نطاق واسع، كان عالم رياضيات أوروبي في العصور الوسطى كتب ليبر أباتشي (كتاب الحساب) في عام 1202 م. في هذا الكتاب ناقش مجموعة متنوعة من المواضيع بما في ذلك كيفية تحويل العملات والمقاييس للتجارة، وحسابات الربح والفائدة، وعدد من المعادلات الرياضية والهندسية، ناقش فوائد استخدام النظام العددي العربي، وفي ذلك الوقت، كان تأثير الإمبراطورية الرومانية المنحلة لا يزال قويا، وكان تفضيل معظم المواطنين الأوروبيين استخدام الأرقام الرومانية ومع ذلك.

في ليبر أباتشي، قدمت فيبوناتشي حجة قوية جدا ومؤثرة، وسهلة الفهم لاستخدام النظام العددي العربي. من تلك النقطة فصاعدا، حصل النظام العددي العربي على موطئ قدم قوي في المجتمع الأوروبي وسرعان ما أصبح الأسلوب السائد للرياضيات في المنطقة وفي نهاية المطاف في جميع أنحاء العالم. كان قويا جدا لدرجة أننا ما زلنا نستخدم النظام العددي العربي حتى يومنا هذا. وقام بتقديم متوالية فيبوناتشي وهي سلسلة من الأرقام حيث كل رقم في السلسلة يعادل مجموع الرقمين السابقين له.

متوالية فيبوناتشي

وتنشأ المتوالية من سلسلة الأرقام التالية: 144 ، 89 ، 55 ، 34 ، 21 ، 13 ، 8 ، 5 ، 3 ، 2 ، 1 ، 1 ، 0
هذه السلسلة من الأعداد مشتقة من 0 تليها 1 ثم تضيف 0 + 1 للحصول على 1 ، الرقم الثالث، ثم إضافة الرقمين الثاني والثالث (1 + 1) للحصول على 2 ، والرقم الرابع ، وهكذا..
تسلسل فيبوناتشي مهم جدا لهذه المناقشة لأننا نحتاج تلك الأرقام للحصول على نسب فيبوناتشي لدينا. بدون تسلسل فيبوناتشي، نسب فيبوناتشي لن تكون موجودة.

دعونا ننظر إلى ما هي نسبة فيبوناتشي، كيف يتم إنشاؤها، وبعض الأمثلة على تلك التي ليست في الواقع نسب فيبوناتشي على الإطلاق.

نسب فيبوناتشي

كل ما علينا فعله هو أخذ أرقام معينة من تسلسل فيبوناتشي واتباع نمط من التقسيم في جميع أنحاء ذلك. على سبيل المثال، دعونا نأخذ عددا في التسلسل ونقسمه على العدد الذي يليه.

0 ÷ 1 = 0
1 ÷ 1 = 1
1 ÷ 2 = 0.5
2 ÷ 3 = 0.67
3 ÷ 5 = 0.6
5 ÷ 8 = 0.625
8 ÷ 13 = 0.615
13 ÷ 21 = 0.619
21 ÷ 34 = 0.618
34 ÷ 55 = 0.618
55 ÷ 89 = 0.618

هل لاحظتِ نمط متطور هنا؟ بدءا من 21 مقسوما على 34 الخروج إلى اللانهاية سوف تحصل دائما على 0.618! يمكننا القيام بذلك مع أرقام أخرى في تسلسل فيبوناتشي أيضا. على سبيل المثال بأخذ رقم في التسلسل وتقسيمه على العدد الذي يسبقه، نرى عدد ثابت آخر يتطور..

1 ÷ 0 = 0
1 ÷ 1 = 1
2 ÷ 1 = 2
3 ÷ 2 = 1.5
5 ÷ 3 = 1.67
8 ÷ 5 = 1.6
13 ÷ 8 = 1.625
21 ÷ 13 = 1.615
34 ÷ 21 = 1.619
55 ÷ 34 = 1.618
89 ÷ 55 = 1.618
144 ÷ 89 = 1.618

نمط آخر يتطور من أعداد تسلسل فيبوناتشي. الآن 1.618 في الواقع يحمل أهمية أكبر لأنه يسمى أيضا النسبة الذهبية، الرقم الذهبي.

أهم مستويات تصحيح الفيبوناتشي؟

• 23.6٪
• 38.2٪
• 50٪
• 61.8٪
• 100٪

مستويات تصحيح الفيبوناتشي هي خطوط أفقية تشير إلى مستويات الدعم والمقاومة المحتملة حيث يمكن أن يؤدي السعر إلى عكس الاتجاه وتتلخص الفكرة في الدخول شراء من مستويات دعم الفيبوناتشي أثناء الاتجاه الصاعد، والدخول بيع من مستويات مقاومة الفيبوناتشي أثناء الاتجاه الهابط.

وتعتبر مستويات الفيبوناتشي مؤشرا تقنيا تنبؤيا لأنها تحاول تحديد مكان السعر في المستقبل، والنظرية هي أنه بعد أن يبدأ السعر اتجاهاً جديداً، سيعود السعر أو يعود مرة أخرى إلى مستوى سعري سابق قبل أن يستأنف اتجاهه.

طريقة رسم مستويات الفيبوناتشي

تختلف طريقة رسم مستويات الفيبوناتشي أثناء الاتجاه الصاعد عن الاتجاه الهابط.

1 – الاتجاه الصاعد
يتم رسم مستويات الفيبوناتشي في الاتجاه الصاعد من الأسفل إلى الأعلى من بداية الحركة الصاعدة ” من القاع إلى القمة” بحيث يكون المستوي صفر بالأعلى والمستوي 100 بالأسفل.

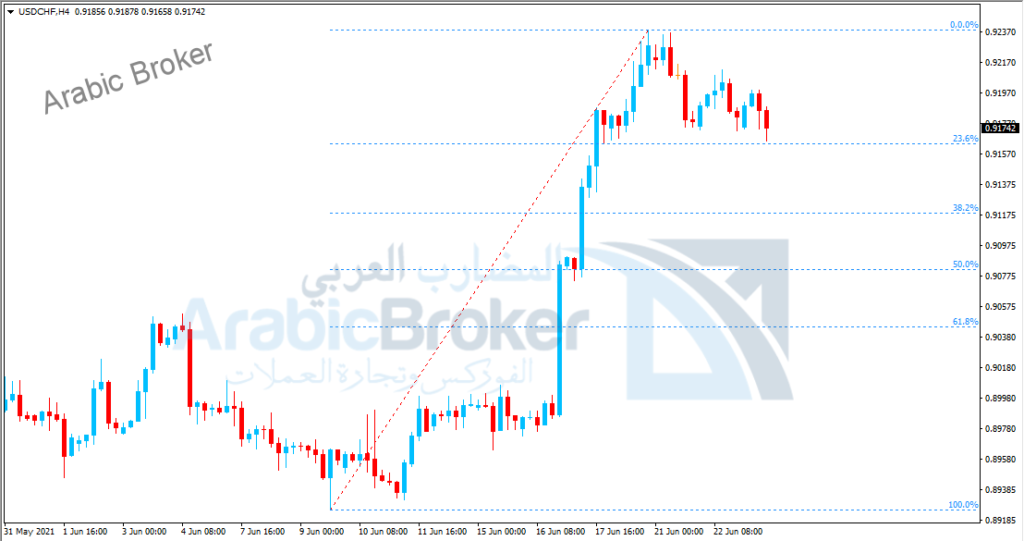
2 – الاتجاه الهابط
يتم رسم مستويات الفيبوناتشي في الاتجاه الهابط من الأعلى إلى الأسفل من بداية الحركة الهابطة ” من القمة إلى القاع” بحيث يكون المستوي صفر بالأسفل والمستوي 100 بالأعلى.

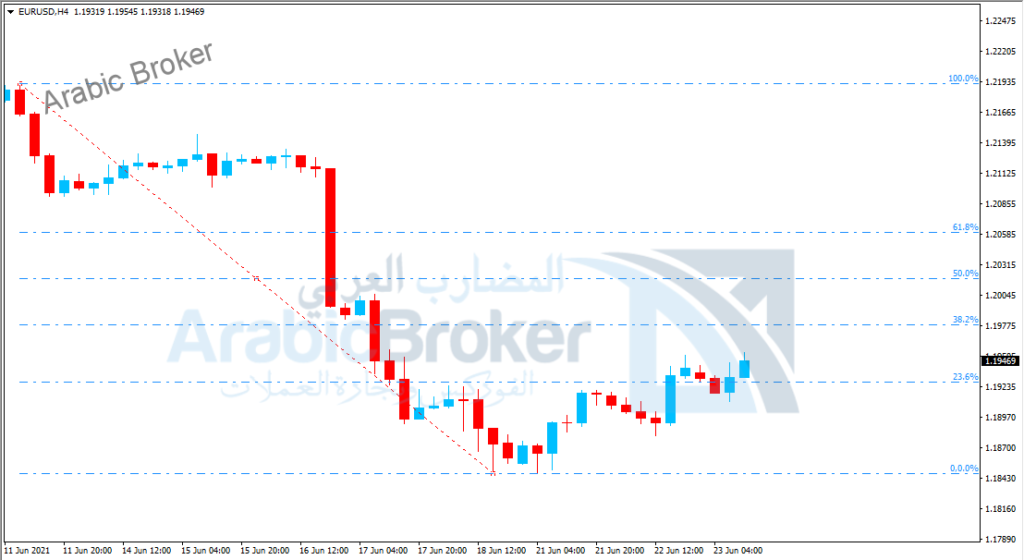
وتمثل مستويات 38.2% و50.0% و61.8% و78.6% النسب التصحيحية المتوقعة لانتهاء تصحيح السعر.

ويستخدم التجار مستويات الفيبوناتشي كمناطق دعم ومقاومة محتملة لتحديد أهداف الربح ومرة أخرى، بما أن العديد من تجار الفوركس يراقبون هذه المستويات ويقدمون طلبات الشراء والبيع للحصول على الأرباح ، فإن هذه المستويات قد تصبح في كثير من الأحيان نهاية لحركة الاتجاه بسبب التوقعات التي تحقق ذاتها.